regression

regression.pdf.pdf)

Machine Learning(机器学习)

一句话概括:机器学习就是让计算机具备找一个函数的能力。

分类：

Regression : 找一个函数，他的输出是一个数值。

classification : 函数的输出是从设定好的选项里选择一个作为输出

structured Learning : 机器产生有结构的东西的问题——学会创造。

Case Study:预测频道流量

找到函数的三个步骤

• Fuction with Unknown Parameters写一个带有未知参数的函数 （model）

y是我们准备要预测的东西（Label），x_1是这个频道前一天总共观看的人数跟数值(feature与w直接相乘)，b和w是未知的参数，它们是准备要透过资料去找出来的参数(weight & bias)

猜测：未来点击阅读次数的函数F,是前一天的点阅次数，乘上w，再加上b(猜测往往来自于对这个问题本质的了解)

• Define Loss from Training Data

Loss也是一个Fuction,它的输入是Model里面的参数

物理意义：Function输出的值代表,现在如果我们把这一组未知的参数,设定某一个数值的时候,这笔数值好还是不好。L越大,代表一组参数越不好,这个大L越小,代表现在这一组参数越好

计算方法：求取估计的值跟实际的值（Label） 之间的差距

MAE(mean absolute error) 、MSE(mean square error) 、 Cross-entropy

Optimization（优化）

梯度下降法

Liner Model(线性模型)

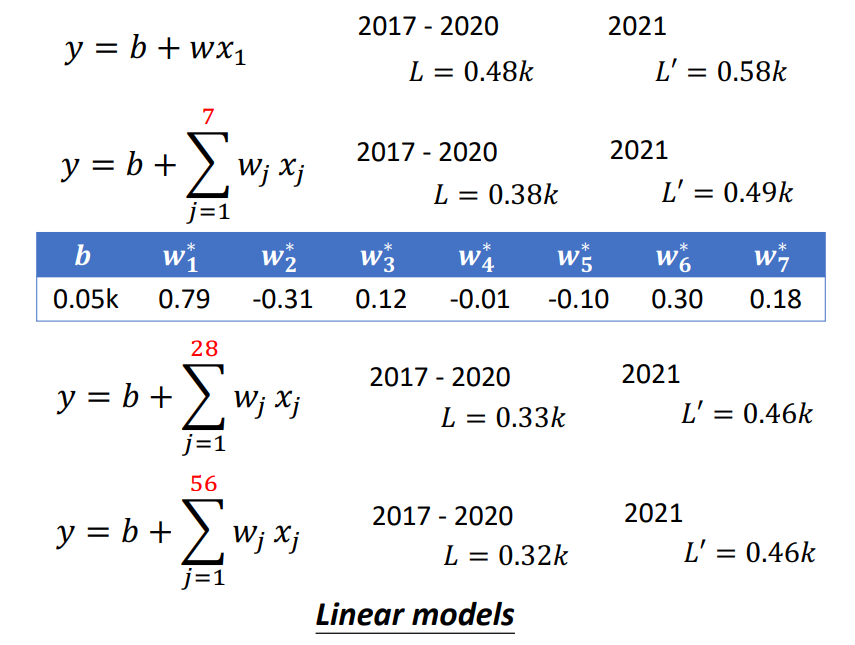
Model的Bias：一个模型无法模拟/描述真实的情况。比如线性模型在高维也只可以是一个超平面，永远无法拟合曲面。

解决方案 ： 需要一个更复杂的、更有弹性的、有未知参数的fuction

Piecewise Linear Curves

Sigmoid函数的意义

1. 模型定义

定义：由多段锯齿状的线段所组成的线

⇒可以看作是一个常数,再加上一堆蓝色的 Function（Hard Sigmoid)

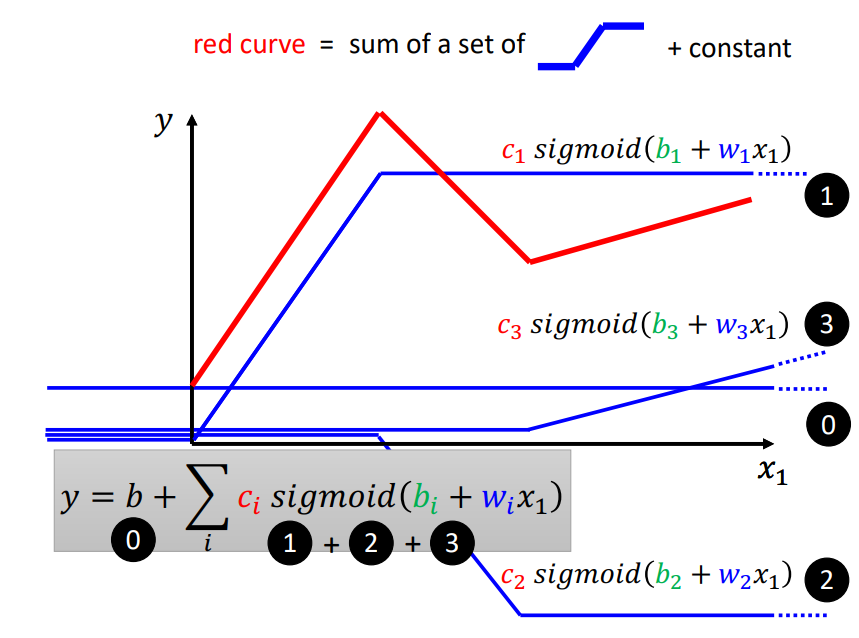
用一条曲线来近似描述这条蓝色的曲线:Sigmoid函数（S型的function）

【事实上，sigmoid的个数就是神经网络中的一层的neuron节点数(使用几个sigmoid是超参数）】

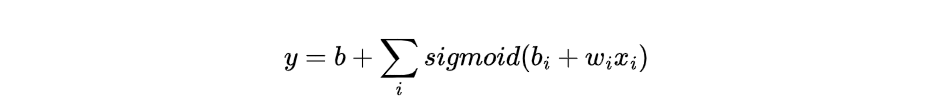
结论：

1. 可以用 Piecewise Linear 的 Curves,去逼近任何的连续的曲线。
2. 每一个 Piecewise Linear 的 Curves,都可以用一大堆蓝色的 Function加上一个常量组合起来得到。
3. 只要有足够的蓝色 Function 把它加起来,就可以变成任何连续的曲线。

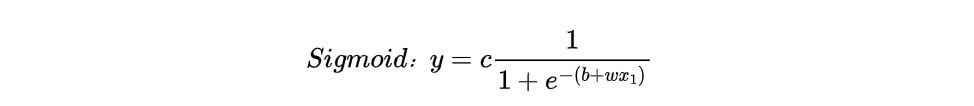
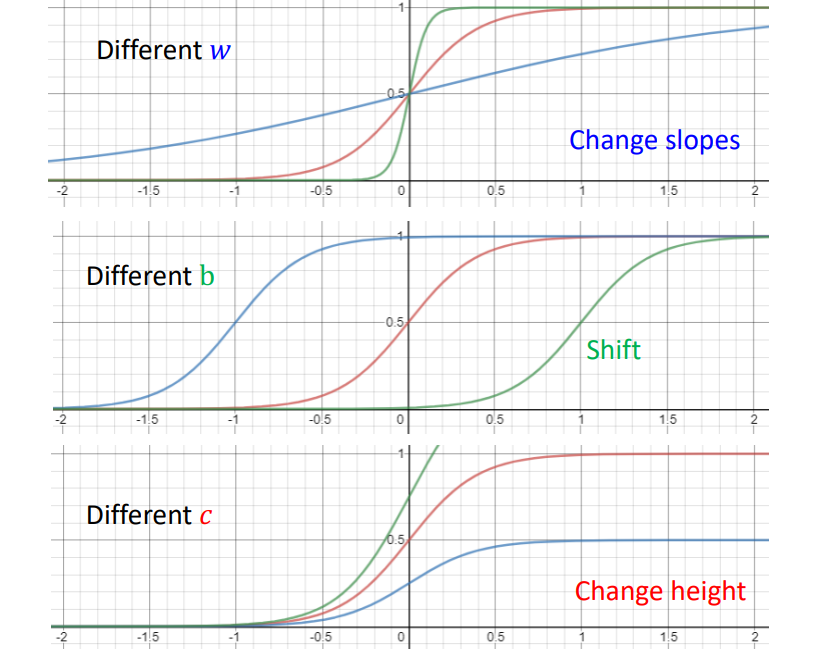
2. 多个特征模型

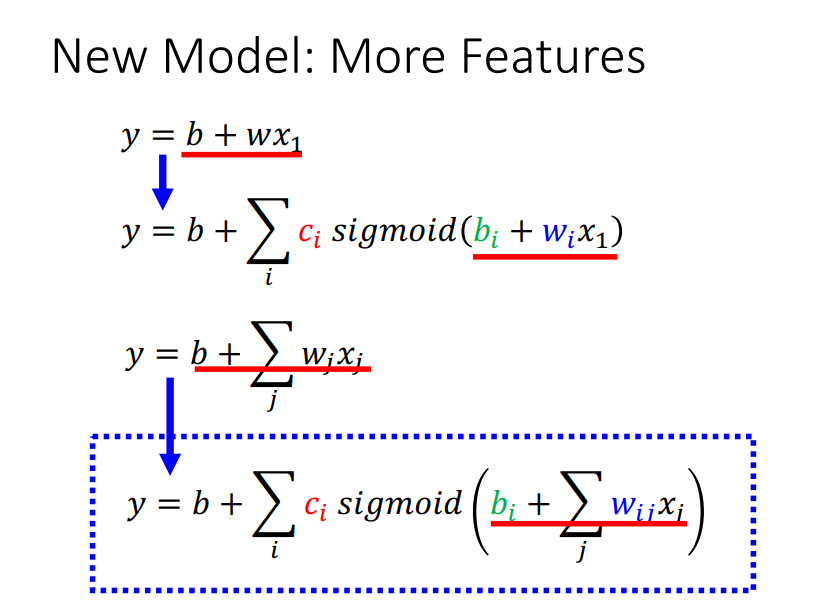
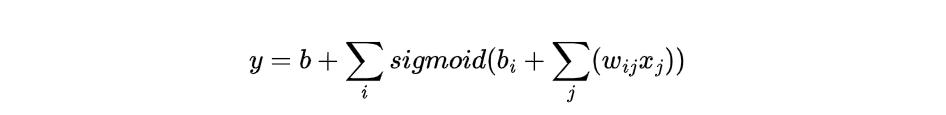
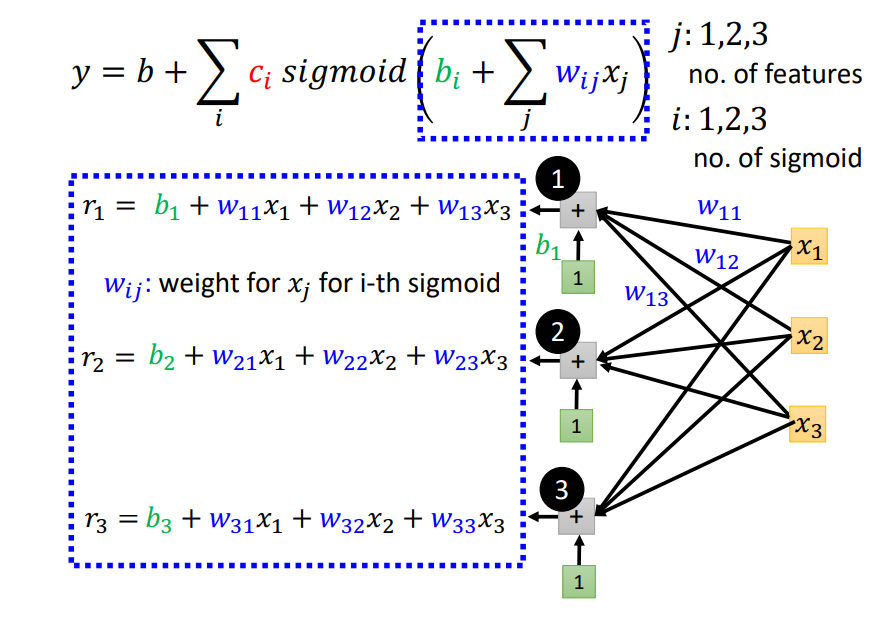
转化为矩阵运算＋激活函数的形式：

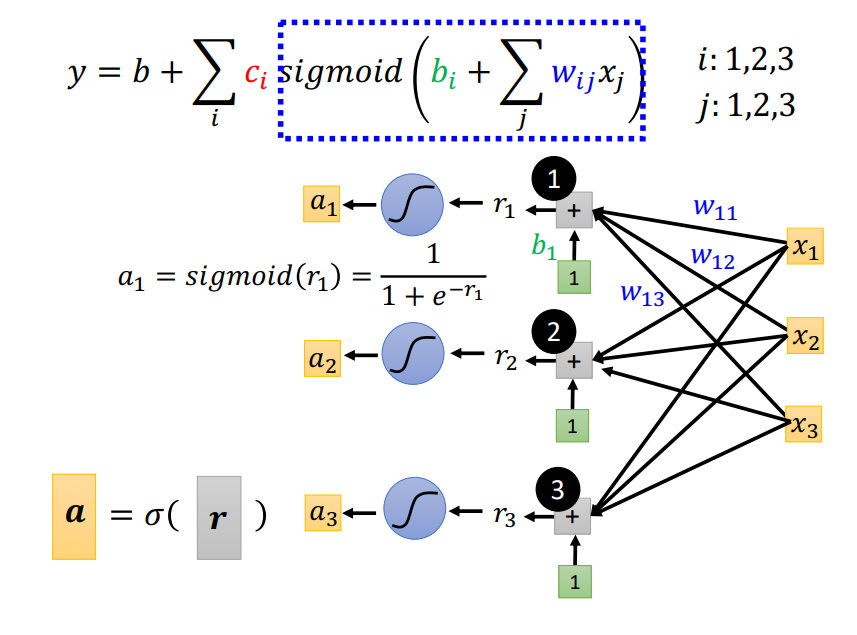
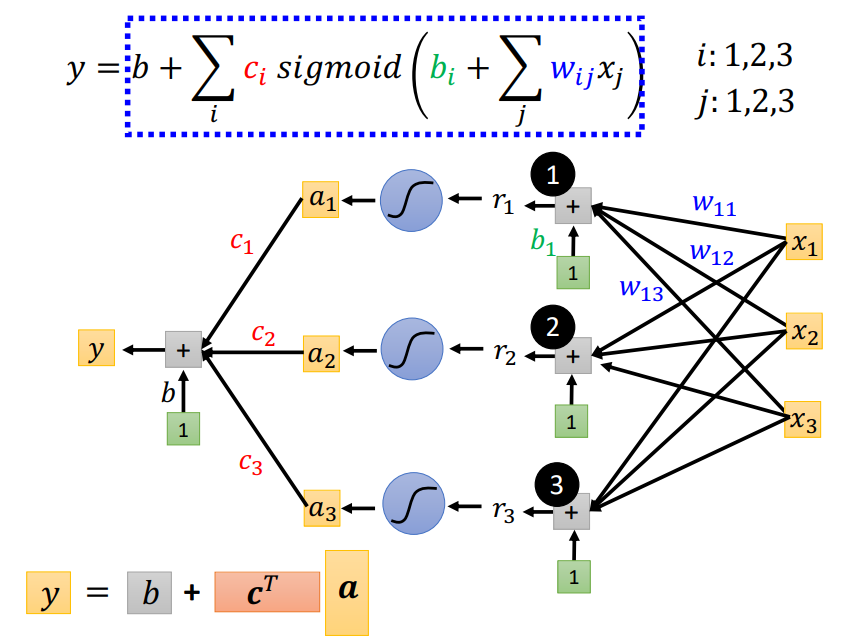
总之：

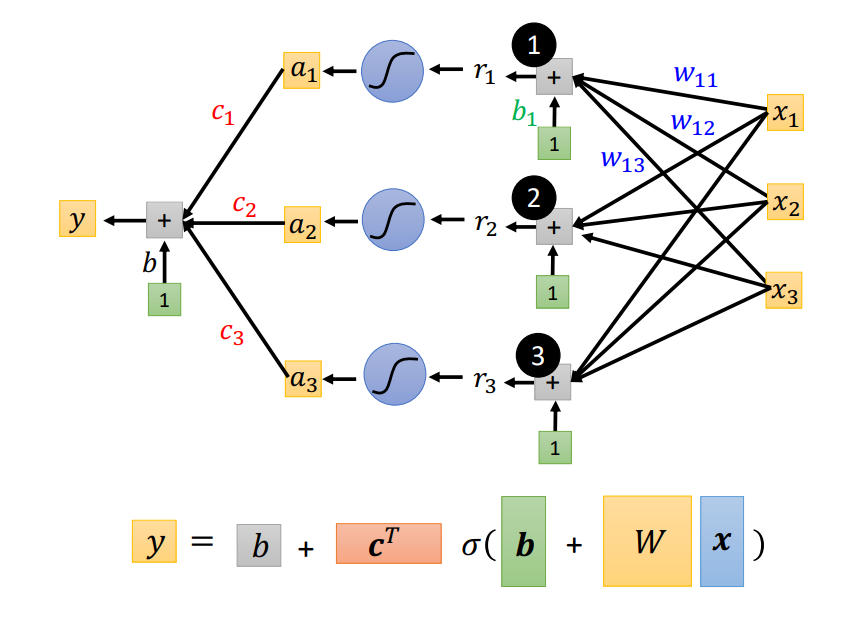
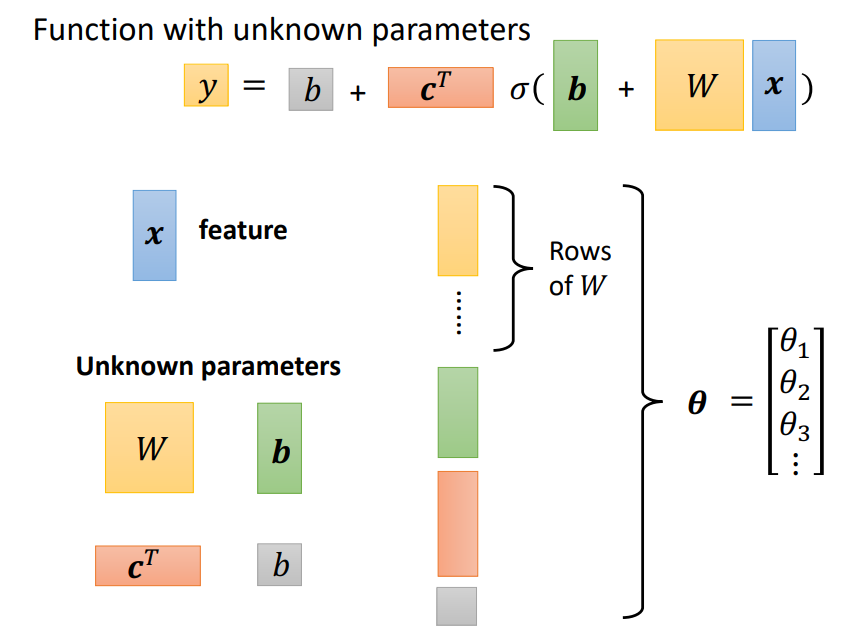
Function with unknown parameters

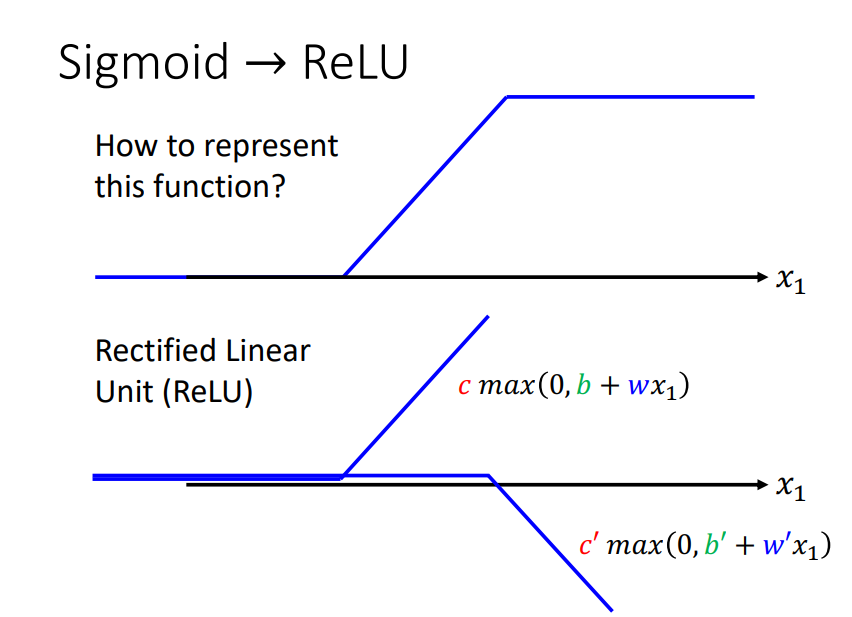
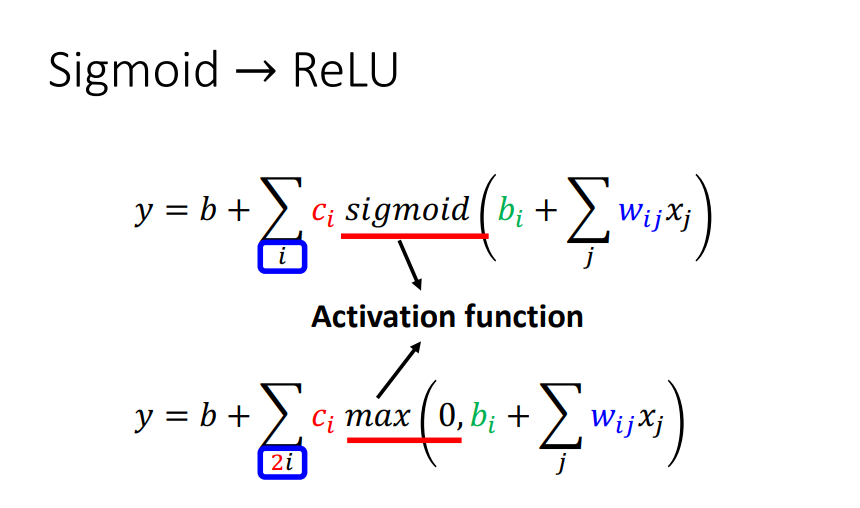
ReLU